Простий гармонійний рух
Простий гармонійний рух – це рух, у якому сила опору руху пропорційна переміщенню.
Простий гармонійний рух продовжується нескінченно довго, оскільки не враховуються сили тертя чи інші сили. Звичайно, це ідеалізований варіант, який не зустрічається у повсякденному житті.
Як приклад простого гармонійного руху розглянемо рух вантажу, прикріпленого до пружини.
У початковий момент часу, коли на вантаж не діють жодні сили, вантаж і пружина перебувають у стані спокою (рівноваги).
Якщо вантаж відтягнути вниз, розтягнувши пружину, а потім відпустити, в пружині виникає пружна сила опору, під дією котрої пружина починає стискатися, а вантаж – рухатися вгору, прагнучи повернутися в положення рівноваги.
Коли вантаж досягне точки положення рівноваги, він матиме деяку швидкість (імпульс), і продовжить рух далі, стискаючи пружину до деякого значення.
Після того, як сили врівноважуються, вантаж перебуватиме в крайній верхній точці, після чого пружна сила пружини змусить пружину розпрямлятися, і вантаж піде вниз, пройде точку положення рівноваги, і досягнувши крайньої нижньої точки знову піде вгору.
У нашому експерименті ми не враховуємо силу тертя, силу тяжкості то опору повітря, вплив яких поступово призведе до того, що амплітуда руху вантажу ставатиме все менше і менше, поки вантаж і пружина не замруть у точці рівноваги.
Якщо ж на систему вантаж+пружина не впливатимуть жодні сторонні сили, то коливання вантажу буде нескінченним.
Періодичні рухи подібного роду називаються періодичними коливаннями, а відстань між крайніми положеннями тіла – амплітудою коливання.
Якщо розглянути рух пружини з вантажем у часі, можна помітити, що вантаж рухається по синусоїдальній кривій.
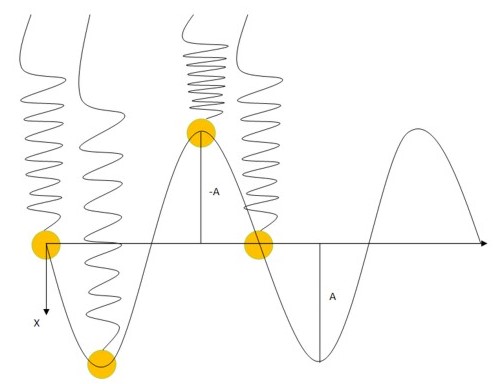
Вантаж здійснюватиме періодичні рухи вгору-вниз, щодо вихідного положення рівноваги, з амплітудою А. Поблизу точки рівноваги вантаж матиме максимальну швидкість, а в точках максимальної амплітуди швидкість вантажу буде нульовою.
Гармонійний обертальний рух
Аналогічну синусоїдальну криву описуватиме вантаж, що рухається по колу, розташованому перпендикулярно площині екрану.
Якщо розташувати коло паралельно площині екрана, то положення вантажу можна визначити за формулою: x=A(cosΘ) (див. рисунок нижче):
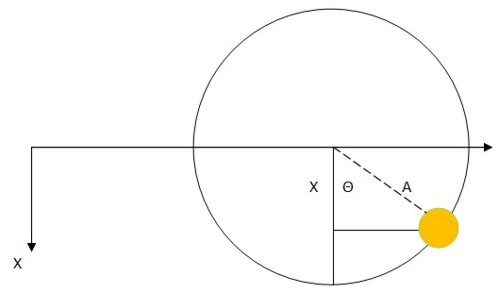
- x – поточне зміщення вантажу по осі Х від положення рівноваги;
- Θ – кут повороту вантажу при обертанні по колу;
- А – амплітуда періодичного руху.
Якщо кутова швидкість руху вантажу по колу постійна, то:
![]()
Цикл обертального руху – це шлях, що дорівнює довжині кола, пройдений вантажем.
Період обертального руху – це час проходження одного циклу.
На малюнках вище повний цикл дорівнює руху вантажу від точки рівноваги (первісне положення) до нижньої точки (А), потім, до верхньої точки (-А), і знову до точки рівноваги (повна синусоїда).
Таким чином, можна стверджувати, що за один повний цикл вантаж проходить кут, що дорівнює 2π за період Т, при цьому кутова швидкість вантажу дорівнює:
![]()
Однією з найважливіших характеристик періодичного руху є його частота – кількість циклів за одиницю часу: f=1/T
Як видно з формули, частота є величиною, обернено пропорційною періоду. Наприклад, якщо за 1 с об’єкт здійснює 10 повних циклів (обертів), то кажуть, що об’єкт обертається з частотою 10 с-1 або з періодом 0,1 с.
Виходячи з вищесказаного, знаходимо зв’язок між частотою та кутовою швидкістю:
![]()
Кутову швидкість при описі періодичних рухів прийнято називати циклічною частотою.

