Закон збереження моменту імпульсу

Закон збереження моменту імпульсу:

Момент імпульсу зберігається у разі, якщо сума всіх моментів зовнішніх сил дорівнює нулю.

Наочне використання моменту імпульсу можна бачити під час виступу фігуристів, коли вони починають обертання з широко розставленими руками, поступово стуляючи руки, вони збільшують швидкість свого обертання. Таким чином, вони зменшують свій момент інерції та збільшують свою кутову швидкість обертання. Таким чином, знаючи початкову кутову швидкість обертання ω₀ та його момент інерції з розведеними I₀ та зімкнутими руками I₁, використовуючи закон збереження моменту імпульсу, можна знайти кінцеву кутову швидкість ω₁:

Застосовуючи закон збереження імпульсу, можна просто розраховувати параметри орбітального руху планет і космічних апаратів.

На сторінці “Закон всесвітнього тяжіння” ми проводили розрахунок лінійної швидкості руху Місяця по орбіті радіусом 392 500 км (середнє значення). Але, як відомо, Місяць рухається еліптичною орбітою, яка в перигеї становить 356400 км, а в апогеї – 406700 км. Використовуючи отримані знання, розрахуємо швидкість Місяця у перигеї та апогеї.

Швидкість  Місяця у перигеї та апогеї

Початкові дані:

• r_ср = 392500 км;
• v_ср = 3600 км/год;
• r_п = 356400 км;
• v_п – ?;
• r_а = 406700 км;
• v_а – ?

Відповідно до закону збереження імпульсу, маємо таку рівність:

Оскільки діаметр Місяця (3476 км) малий у порівнянні з відстанню до Землі, вважатимемо Місяць матеріальною точкою, що значно спростить розрахунки, не вплинув на їх точність.

Моменти інерції для матеріальної точки дорівнюватимуть:

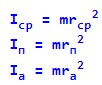
Кутові швидкості:

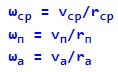
Проведемо відповідні підстановки у формулу закону збереження імпульсу:

Виконавши нескладні перетворення, отримаємо:

Підставляємо числові значення:

Таким чином, швидкість Місяця в перигеї складає 3964 км/год, а в апогеї = 3474 км/год. Як бачимо, різниця досить суттєва = 490 км/год.

Репетитор з математики Ірпінь (онлайн Zoom)