Графік функції
Для будь-якої функції може бути збудований її графік.
Площина, в якій побудовано прямокутну систему координат, називається координатною площиною.
Будь-яка точка координатної площини має свої координати – певне значення абсциси (координата x) і ординати (координата y).
Множину точок на координатній площині, котра виділена якимось чином, називають графіком.
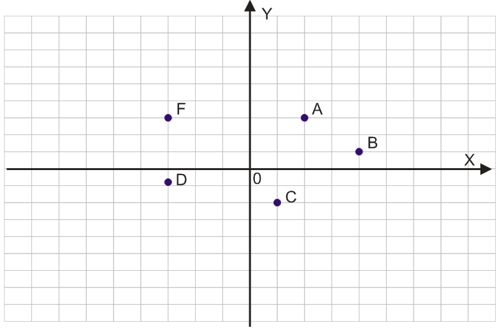
На малюнку показаний графік, що складається з 5 точок, що мають наступні координати (x, y):

Графік функції може складатися з кінцевого числа точок, але, частіше графік включає безліч точок у вигляді лінії.
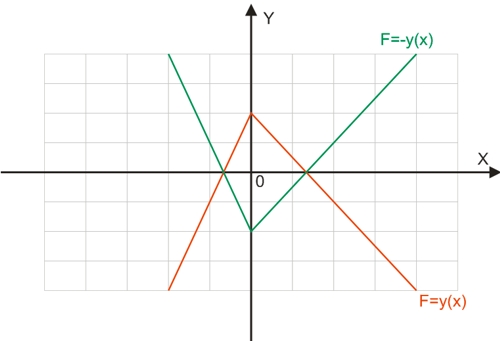
Якась лінія буде графіком функції F=y(x) у разі, якщо кожному значенню аргументу x відповідатиме єдине значення залежної змінної y.
Раніше вже було сказано про три способи завдання функцій: формулою, таблицею, власне графіком.
Найчастіше функція визначається за допомогою формули, в якій ординати точок графіка функції знаходяться після підстановки у формулу відповідних абсцис цих точок.
Розглянемо графік абстрактної функції F=y(x), показаної на малюнку нижче.
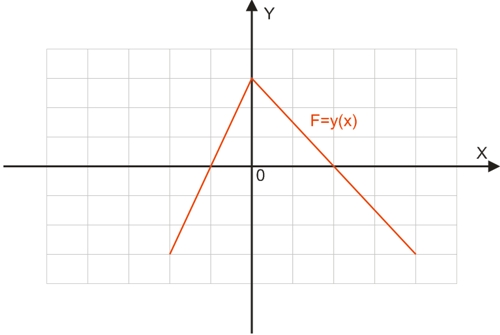
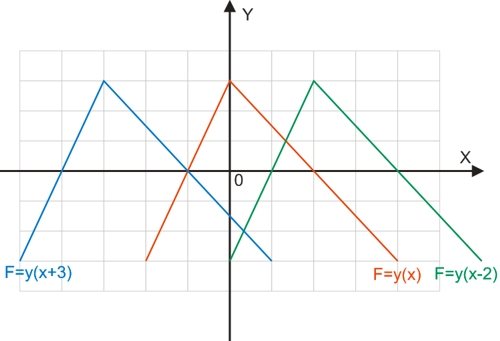
Графік функції F=±a + y(x) вийде шляхом зсуву графіка функції (червоний колір) вздовж осі ординат вгору (при позитивному – зелений колір) або вниз (при негативному – синій колір).
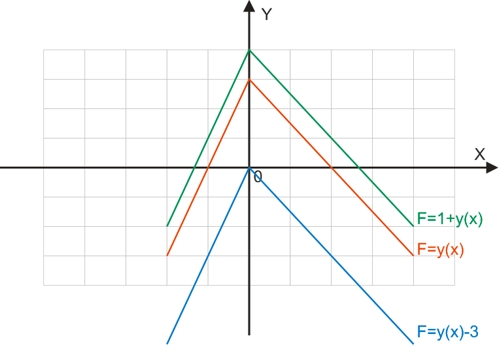
Графік функції F=y(x±b) вийде шляхом зсуву графіка функції (червоний колір) вздовж осі абсцис вліво (при позитивному b – синій колір) або вправо (при негативному b – зелений колір).
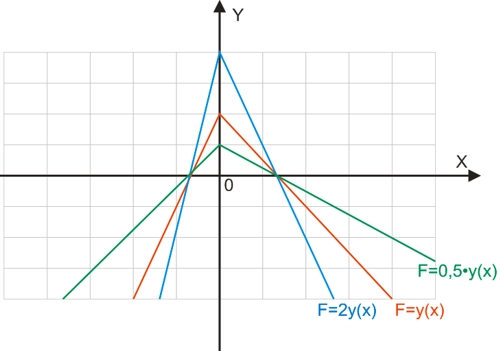
Графік функції F=m·y(x) вийде шляхом стиснення (0<m<1 – зелений колір – точки графіка як би зближуються з віссю абсцис) або розтягування (m>1 – синій колір – точки графіка як би віддаляються від осі абсцис ) графіка первинної функції (червоний колір) від осі абсцис вздовж осі ординат у m разів.
Графік функції F=-y(x) є дзеркальним відображенням графіка (червоний колір) щодо осі абсцис.