Обертальний рух та другий Закон Ньютона
Згідно з другим законом Ньютона, прискорення тіла під дією сили пропорційно величині сили і обернено пропорційно масі об’єкта:
![]()
Задамося питанням, чи діє другий закон Ньютона для обертального руху?
Використовуючи аналоги характеристик поступального та обертального рухів другий закон Ньютона для обертального руху матиме вигляд:
![]()
- роль прискорення виконує кутове прискорення α;
- роль сили F – момент сили М;
- масу m – замінює момент інерції I.
Припустимо, що тіло рухається по колу під дією прикладеної по дотичній прямій до кола тангенціальною силою, яка призводить до збільшення тангенціальної швидкості м’ячика (не плутати з нормальною силою), спрямованою вздовж радіуса кола обертання (докладно тангенціальна та нормальна швидкість розглянута на сторінці “Параметри обертального руху“).
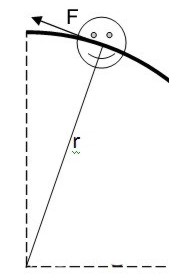
Помножимо обидві частини рівності, що описує другий закон Ньютона, на радіус кола r:
![]()
Як відомо, Fr=М, тому:
![]()
Таким чином, ми здійснили перехід від другого закону Ньютона для поступального руху до його аналога для руху обертального. Слід зазначити, що ця формула справедлива лише для матеріальної точки, для протяжного об’єкта необхідно використовувати інші формули, які будуть розглянуті пізніше.
Щоб завершити перехід від опису поступального руху до обертального, використовуємо зв’язок між кутовим прискоренням і тангенціальним прискоренням а:
![]()
Здійснюємо підставку однієї формули в іншу і отримуємо:

Отримана формула пов’язує момент сили, що діє матеріальну точку, та її кутового прискорення. Зв’язок здійснюється через коефіцієнт пропорційності mr2, який називають моментом інерції матеріальної точки і позначають I (вимірюється в кгм2).
У результаті ми отримали еквівалент другого закону Ньютона для обертального руху:
![]()
У тому випадку, якщо на тіло діє одночасно кілька сил, другий закон Ньютона набуває такого вигляду:
![]()
ΣF – векторна сума всіх сил, що діють на об’єкт.
У випадку, якщо на об’єкт діють одночасно кілька моментів сил, другий закон Ньютона набуде вигляду:
![]()
ΣМ – векторна сума всіх моментів сил, що діють на об’єкт.

