Тертя на похилій площині
Завдання №1: яка сила буде потрібна для підняття кулі масою 1 кг по похилій площині, розташованій під кутом α=30° до горизонту. Коефіцієнт тертя μ = 0,1
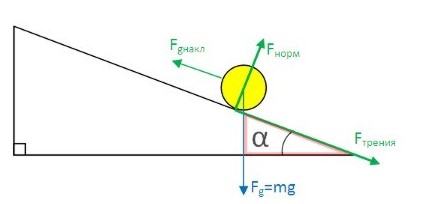
Обчислюємо складову сили тяжіння. Для початку нам треба дізнатися кут між похилою площиною та вектором сили тяжіння. Подібну процедуру ми робили, розглядаючи гравітацію.
Сила тяжіння спрямована вертикально донизу. Сума кутів будь-якого трикутника дорівнює 180 °. Розглянемо трикутник, утворений трьома силами: вектор сили тяжіння; похилою площиною; основою площини (на малюнку він виділений червоним кольором).
- Кут між вектором сили тяжіння та основою площину дорівнює 90°.
- Кут між похилою площиною та її основою дорівнює α
Тому кут, що залишився – кут між похилою площиною і вектором сили тяжіння:
![]()
Складові сили тяжіння вздовж похилої площини:
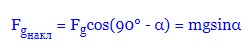
Необхідна сила для підняття кулі:
F = Fgнакл + Fтертя = mgsinα + Fтертя
Необхідно визначити силу тертя Fтр. З урахуванням коефіцієнта тертя спокою:
Fтертя = μFнорм
Кут між площиною та силою тяжіння
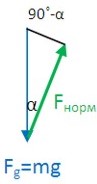
Обчислюємо нормальну силу Fнорм, яка дорівнює складовій силі тяжіння, перпендикулярно спрямованої до похилої площини. Ми вже знаємо, що кут між вектором сили тяжіння та похилою площиною дорівнює 90°-α.
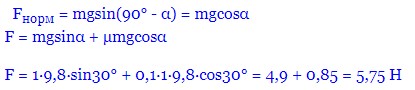
Нам потрібно до кулі докласти силу в 5,75 Н для того, щоб закотити її на вершину похилої площини.
Завдання №2: визначити як далеко прокотиться куля масою m = 1 кг горизонтальною площиною, скотившись по похилій площині довжиною 10 метрів при коефіцієнті тертя ковзання μ = 0,05
Сили, що діють на кулю, що скачується, наведені на малюнку.
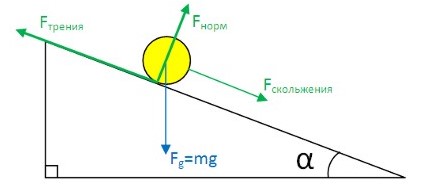
Складна сили тяжіння вздовж похилої площини:
![]()
Нормальна сила:
![]()
Сила тертя ковзання:
Fтертя = μFн = μmgsin(90° – α) = μmgcosα
Результуюча сила:

Визначаємо швидкість кулі в кінці похилої площини:
![]()
Куля закінчує рух похилою площиною і починає рух горизонтальною прямою зі швидкістю 9,5 м/с. Тепер у горизонтальному напрямку на кулю діє лише сила тертя, а складова сили тяжіння дорівнює нулю.
Сумарна сила:
![]()
Знак мінус говорить про те, що сила спрямована у протилежний бік від руху. Визначаємо прискорення уповільнення кулі:
![]()
Гальмівний шлях кулі:
![]()
Оскільки ми визначаємо шлях кулі до зупинки, то V1=0:
![]()
Наша кулька прокотилася по прямій цілих 92 метри!

