Подібні трикутники. Які трикутники називаються подібними
Подібні трикутники – це трикутники, у котрих їх кути відповідно дорівнюють одне одному, а подібні сторони – пропорційні.
У трикутниках, у яких рівні кути, відповідними називаються сторони, що протилежні відповідним кутам.
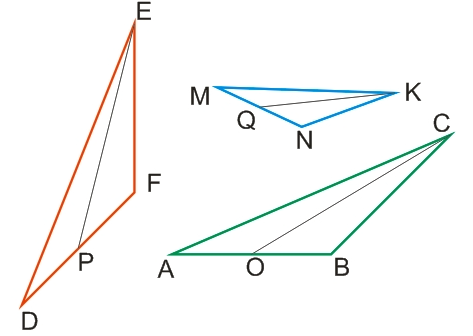
На малюнку трикутники ABC, DFE, MNK подібні, тому що:
- ∠A=∠D=∠M – відповідні кути;
- ∠B=∠F=∠N – відповідні кути;
- ∠C=∠E=∠K – відповідні кути;
- подібні сторони AB, DF, MN – пропорційні;
- подібні сторони BC, FE, NK – пропорційні;
- подібні сторони CA, ED, KM – пропорційні.
Говорячи “життєвою мовою”, подібні трикутники виходять шляхом зміни масштабу та/або обертання навколо осі.
Коефіцієнт подібності – відношення подібних сторін таких трикутників.
- Коефіцієнт подібності трикутників АВС та DFE дорівнює 1, оскільки AB/DF=BC/FE=CA/ED=1.
- Коефіцієнт подібності трикутників ABС та MNK: AB/MN=BC/NK=CA/KM=3/2.
Медіани, бісектриси та висоти, проведені до подібних сторін у подібних трикутників, називаються подібними.
У подібних трикутників відношення подібних медіан, як і відношення подібних висот, як і відношення подібних бісектрис дорівнює коефіцієнту подібності.
- AB/DF=BC/FE=CA/ED=CO/EP=1.
- AB/MN=BC/NK=CA/KM=CO/KQ=3/2.
Площі подібних трикутників дорівнюють квадрату коефіцієнта подібності.
Трикутники будуть подібними, якщо:
- вони мають дві пари рівних кутів (якщо ∠A=∠D; ∠B=∠F, то трикутники ABC та DFE подібні – див. рисунок вище);
- вони мають одну пару рівних кутів, до яких належать пропорційно рівні сторони (якщо ∠A=∠D; AB/DF=AC/DE, то трикутники ABC та DFE подібні – див. рисунок вище);
- всі сторони одного трикутника пропорційні сторонам іншого (AB/DF=BC/FE=CA/ED, трикутники ABC і DFE подібні – див. малюнок вище).

