Функції виду y=x; y=kx
Функція виду y=x
- Область визначення функції y=x – область всіх дійсних чисел;
- Функція y=x зростає по всій області визначення;
- Графік функції y=x проходить через початок координат;
- Функція y=x непарна, її графік симетричний щодо початку координат;
- Функція y=x перестає бути періодичною функцією.
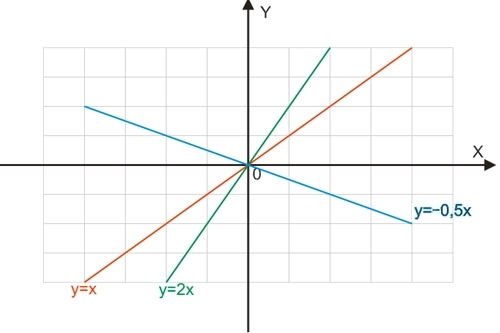
Функція виду y=kx
Функція y=kx називається прямою пропорційністю.
- Область визначення функції y=kx – область всіх дійсних чисел;
- Функція y=kx зростає по всій області визначення при k>0 і зменшується при k<0; при k=0 графік функції збігається з віссю абсцис;
- Графік функції y=kx проходить через початок координат;
- Функція y=kx непарна, її графік симетричний щодо початку координат;
- Функція y=kx не є періодичною функцією.
Лінійна функція y=kx+b
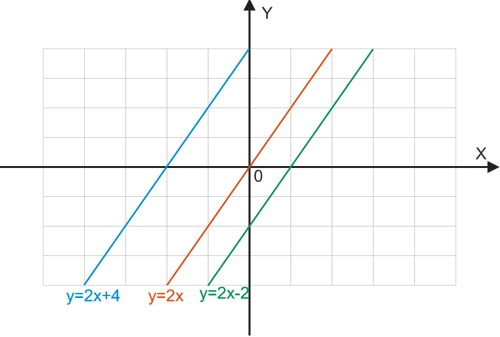
Розглянуті вище функції y=x та y=kx є окремим випадком лінійної функції y=kx+b:
![]()
Графік лінійної функції y=kx+b виходить у результаті паралельного зсуву графіка функції y=kx на b одиниць вздовж осі ординат: при b>0 графік зрушується вгору; при b<0 – вниз.
Властивості лінійної функції:
- Область визначення функції y=kx+b – область всіх дійсних чисел;
- Функція y=kx+b зростає по всій області визначення при k>0 і зменшується при k<0;
- При b≠0 функція y=kx+b не є ні парною, ні непарною;
- Функція y=kx+b перестає бути періодичною функцією.

