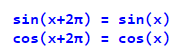Властивості функції
При побудові графіка будь-якої функції слід враховувати її властивості.
Область визначення функції
Допустимі значення, які може набувати аргумент функції, називається її областю визначення.
Наприклад, у функції y=x областю визначення буде множина дійсних чисел.
У функції y=1/x областю визначення буде множина дійсних чисел, не рівних нулю.
У функції y=√x областю визначення буде безліч чисел, що задовольняють нерівності x≥0;
Проміжки зростання та спадання
Функція буде зростаючою на якомусь проміжку, якщо на цьому проміжку більшому значенню аргументу буде відповідати більше значення функції:
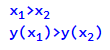
Функція буде спадаючою на якомусь проміжку, якщо на цьому проміжку більшому значенню аргументу буде відповідати менше значення функції:
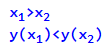
На малюнку, представленому нижче, ліва частина графіка відповідає зростаючій функції (піднімаємося вгору), а права – спадаючій (котимося з гори).
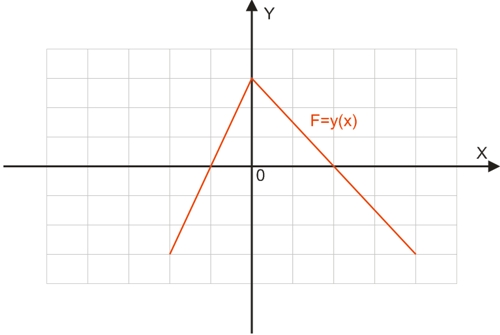
Корінь функції
Коренем функції F=y(x) є точка (точки) у яких графік функції перетинає вісь абсцис: y(x)=0:
- y=x; корінь функції: x = 0;
- y=x+2; корінь функції: x = -2;
- y=x2; корінь функції: x = 0;
- y=x2-1; корінь функції: x = ±1.
- y=x2+1; Функція коренів не має.
Парні та непарні функції
- для парної функції: y(-x)=y(x) – графік парної функції симетричний щодо осі ординат;
- для непарної функції: y(-x)=-y(x) – графік непарної функції симетричний щодо початку координат.
Все сказане вище про парність і непарність функції справедливо для всіх значень аргументу з області визначення.
Більшість функцій не є парними або непарними.
Періодичність функції
Функція називається періодичною, якщо існує деяке число A, при якому для всіх значень аргументу з області визначення буде справедлива рівність:
![]()
Класичними періодичними функціями є функції синуса та косинуса: