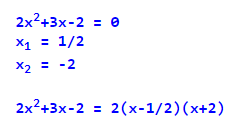Наведене квадратне рівняння
Наведеним називається квадратне рівняння виду:
![]()
“Класичне” квадратне рівняння стає наведеним при А=1, тому будь-яке квадратне рівняння можна записати у вигляді наведеного, для цього треба розділити обидві частини рівняння на перший коефіцієнт А.
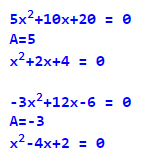
Теорема Вієта
Якщо x1, x2 – коріння квадратного рівняння x2+Bx+C=0, то добуток коренів дорівнюватиме вільному члену, а їх сума – другому коефіцієнту, взятому зі зворотним знаком:
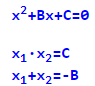
Наприклад:

Теорема, зворотна теоремі Вієта
Якщо сума чисел x1, x2 дорівнює (-В), а їх добуток дорівнює С, то числа x1, x2 є корінням квадратного рівняння x2+Bx+C=0.
Розкладання багаточлена Ax2+Bx+C
Ліву частину квадратного рівняння Ax2+Bx+C=0 можна розглянути, як багаточлен Ax2+Bx+C.
У разі, якщо x1, x2 є корінням цього рівняння, то многочлен розкладається на такі множники:
![]()
Як приклад візьмемо квадратне рівняння, приклад розв’язання якого наведено на сторінці “Яке рівняння називається квадратним“: