Прості та складені числа

Простими натуральними числами називаються числа, які діляться без залишку тільки на одиницю і саму себе.

11:1 = 11;

11:11 = 1

Складеними натуральними числами називаються числа, які мають більше двох натуральних дільників, тобто, крім одиниці і себе ще мають інші дільники, на які діляться без залишку.

14:1 = 14

14:2 = 7

14:7 = 2

14:14 = 1

• 1 (одиниця) – не є ні простим, ні складовим числом, тому, що має лише один натуральний дільник – 1.
• 2 (двійка) – є єдиним парним простим числом.

Будь-яке складове число можна розкласти на прості множники:

100 = 2 · 2 · 5 · 5

Таким чином, можна сказати, що вся безліч натуральних чисел складається з суми двох множин – множини простих чисел і безлічі складових чисел.

Таблиця простих чисел від 1 до 1000

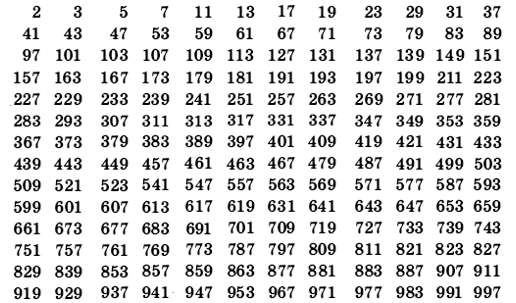
Розкладання складених чисел на прості множники

Розкладання невеликих чисел на прості множники  не складає труднощів. А ось з числами великими ситуація дещо інша.

Щоб розкласти велике число на прості множники, користуються таблицею простих чисел (див. вище) і ознаками подільності чисел.

Порядок розкладання натурального числа на прості множники наступний:

1. за ознаками подільності знаходять перший із простих чисел дільник: 2, 3, 5, 7, 11;
2. наше число поділяється на перший знайдений “простий” дільник, далі продовжують працювати з залишком, що вийшов (див. п.1).

Приклади розкладання натуральних чисел на прості дільники

Як приклад розкладемо на прості дільники число 777:

1. насамперед дивимося в таблицю простих чисел (див. вище) і бачимо, що число 777 не є простим;
2. починаємо пошук найменшого простого дільника;
3. першим простим дільником числа 777 буде число 3 – це зрозуміло, тому, що 2 не підходить, оскільки 777 число непарне, а 3 підходить, і тут навіть не треба складати цифри числа, оскільки в числі 777 є 3 однакові цифри: 777:3=259;
4. знову перевіряємо по таблиці, чи є число 259  простим числом – ні, не є, значить, продовжуємо його розкладання на прості множники;
5. першим простим дільником числа 259 буде число 7: 259: 7 = 37;
6. знову дивимося в таблицю простих чисел, і бачимо, що число 37 є простим числом, отже розкладання закінчено;
7. Результат: 777 = 2 · 7 · 37.

Візьмемо більш складний приклад – число  27359850:

1. Якщо  число закінчується нулем, то відразу є два простих множника, добуток яких дає 10 – це 2 і 5: 2 · 5 = 10;
2. тому, зі старту вже маємо два простих множники 2 і 5, а вихідне число зменшується на 10;
3. працюємо далі з числом 2735985 – це непарне число, тому 2 відкидаємо;
4. сума цифр серед 2735985 кратна 3, отже, наступним простим множником буде 3: 2735985:3=911995;
5. число 91195 не кратне ні 2, ні 3, але кратне 5: 91195:5 = 18239;
6. наступним найменшим простим дільником буде число 13: 18239:13 = 1403;
7. наступним найменшим простим дільником буде число 23: 1403:23 = 61;
8. 61 є простим числом – розкладання закінчено;
9. Результат: 27359850 = 2 · 3 · 5 · 5 · 13 · 23 · 61.

Індивідуальні заняття з математики в режимі онлайн (Zoom)