Момент інерції протяжного об’єкту
Момент інерції досить легко вирахувати для точкового об’єкта, якщо вважати, що всі точки об’єкта знаходяться на однаковій відстані від точки обертання.
Наприклад, можна вважати Землю точковим об’єктом, який рухається орбітою навколо Сонця, оскільки розмір планети набагато менше відстані від Землі до Сонця – діаметр Землі – 12756 км; середня відстань від Землі до Сонця – 150 млн. км. (Приблизно 0,008%).
Формула для обчислення моменту інерції точкового об’єкта має вигляд:
- r – відстань, де від центру обертання зосереджена вся маса об’єкта m.
У прикладних завданнях набагато частіше зустрічається ситуація, коли об’єкт, для якого необхідно обчислити момент інерції, не є точковим, наприклад, стрижень, що обертається навколо одного зі своїх кінців. У такого стрижня маса розподілена по всій його довжині. Як бути у такому разі?
Для визначення моменту інерції протяжних об’єктів проводять підсумовування моментів інерції всіх його матеріальних точок:
Звісно ж, у реальному житті інженеру неможливо обчислити усю безліч матеріальних точок, з яких складається об’єкт, та обчислити момент інерції для кожної такої точки. Сучасна фізика вже зробила роботу, обчисливши моменти інерції багатьох об’єктів, котрі мають стандартну форму. Нижче наведено кілька формул для обчислення моментів інерції деяких стандартних об’єктів:
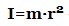– обруч радіуса r, що обертається щодо свого центру в площині обруча (порожнистий циліндр радіуса r, що обертається щодо своєї осі).
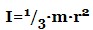– стрижень довжиною r, який обертається щодо осі, розташованої біля одного кінця стрижня і орієнтований перпендикулярно стрижню.
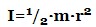– диск радіусом r, який обертається щодо свого центру в площині диска (суцільний циліндр радіусом r, що обертається навколо своєї осі).
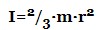– порожниста сфера радіусом r, яка обертається щодо своєї осі.
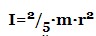– суцільна сфера радіусом r, яка обертається щодо своєї осі.
На конкретних прикладах покажемо порядок розрахунку момена інерції для об’єктів з простою геометрією.
Розкрутка компакт-диска
Ті, хто знайомий з комп’ютерною технікою, повинні знати, що компакт-диски обертаються з різними кутовими швидкостями, забезпечуючи тим самим постійну лінійну швидкість запису-зчитування інформації з диска, яка розташована на різних доріжках, що знаходяться на різних відстанях від центру диска.
Початкові дані:
- Маса компакт-диска – 30 г;
- Діаметр диска – 12 см;
- У початковий момент часу диск обертається з кутовою швидкістю 100 об/хв;
- Через 10 хвилин швидкість диска збільшується до 500 об/хв.
Завдання: обчислити середній момент сил, необхідний збільшення швидкості компакт-диска.
Формула зв’язку моменту сил та кутового прискорення:
Формула розрахунку моменту інерції диска з радіусом r, що обертається щодо свого центру в площині диска (див. вище):
Підставляємо числові значення:
Визначаємо кутове прискорення:
- Δt = 10 хв = 600 с
- ω0 – початкова швидкість компакт-диска = 100·2π = 628 с-1
- ω1 – кінцева швидкість компакт-диска = 500·2π = 3140 с-1
Підставляємо числові значення формули:
Розрахуємо тепер силу, необхідну для створення такого моменту, за умови, що вона буде додана до краю компакт-диска:
