Скалярний добуток векторів
Вектор можна не лише множити на число, а й множити вектори між собою.
Скалярний добуток векторів – це множення двох векторів між собою.
Якщо додавання або віднімання векторів є, загалом, досить зрозумілою і логічною дією, яка просто відображається графічно, то з розумінням скалярного добутку векторів не все так просто. Набагато легше запам’ятати формулу скалярного множення двох векторів, благо, вона набагато простіше для запам’ятовування, ніж для розуміння.
![]()
- скалярний добуток перпендикулярних векторів дорівнює нулю, тому, що cos(90°)=0;
- якщо хоча б один з векторів, що перемножуються, є нульовим, то скалярний добуток також дорівнюватиме нулю;
- якщо жоден з векторів, що перемножуються, не є нульовим, а скалярний добуток векторів дорівнює нулю, то кут між такими векторами буде прямим;
- якщо кут між векторами тупий, то скалярний добуток таких векторів буде від’ємним числом;
- якщо кут між векторами гострий, то скалярний добуток таких векторів буде позитивним числом;
- добуток вектора самого на себе буде дорівнює квадрату модуля цього вектора.
Все ж таки спробуємо роз’яснити суть множення двох векторів.
Почнемо з найпростішого випадку, коли два вектори, що перемножуються між собою, є співспрямованими, тобто, кут між такими векторами дорівнюватиме 0°.
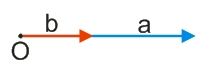
В такому випадку:
![]()
Таким чином, добуток спрямованих векторів дорівнюватиме добутку їх модулів, тобто, множиться довжина одного вектора на довжину другого вектора.
ВАЖЛИВО: Зауважте, що результатом скалярного добутку векторів буде число, а не вектор!
А як бути, якщо вектори, що перемножуються між собою, розташовані під деяким кутом один до одного?
У цьому випадку в справу вступає косинус величини кута, під яким розташовуються один до одного вектори, що перемножуються.
Візьмемо ще один окремий випадок, коли два вектори розташовані перпендикулярно один до одного, тобто утворюють кут 90°.
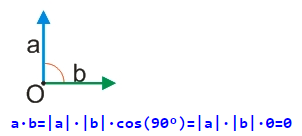
Як бачимо, добуток двох перпендикулярних векторів дорівнює 0.
Чому так відбувається?
Нюанс перемноження двох векторів, розташованих один до одного під деяким кутом, полягає в тому, що перемножується модуль першого вектора на модуль проекції на цей вектор другого вектора. У разі перпендикулярності проекція другого вектора на перший буде точкою або нульовим вектором, а скалярний добуток вектора на нульовий вектор дорівнює нулю (див. вище).
Візьмемо третій можливий випадок, коли кут між векторами гострий, тобто лежить в межах від 0° до 90°.

Як відомо, косинус кутів у цьому діапазоні буде числом позитивним – менше 1, але більше 0. Тому, скалярний добуток двох не нульових векторів, розташованих один до одного під гострим кутом, завжди буде числом позитивним (не слід забувати, що модуль вектора не може бути числом від’ємним, оскільки це відстань між двома точками).
У разі, якщо кут між векторами, що перемножуються, буде тупим, тобто більше 90°, але менше 180°, у такому випадку добуток таких векторів буде числом негативним, оскільки в цьому діапазоні косинус коливається від 0 до -1.
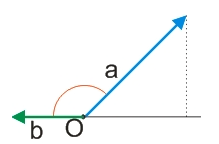
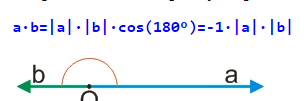
І останній окремий можливий випадок – вектори, що перемножуються, є протилежно спрямованими, тобто, утворюють розгорнутий кут (180°). У такому випадку, оскільки cos(180°)=-1, скалярний добуток протилежно спрямованих векторів дорівнюватиме від’ємному добутку їх модулів.
Скалярний добуток векторів, заданих координатами
Якщо:
- {x1; y1} координати вектора a;
- {x2; y2} координати вектора b;
- то: ab = x1x2 + y1y2
Формула для обчислення довжини вектора з координатами {x;y}:
![]()
Властивості скалярного добутку векторів:
- переміщувальний закон: ab = ba;
- розподільчий закон: (a+b)c = ac+bc;
- поєднаний закон: (ka) b = k (ab), де k – будь-яке число;
- від’ємний квадрат ненульового вектора буде позитивним числом: а-2>0.

