Квадратична функція, графік квадратичної функції
Квадратична функція y=ax2+bx+c
Квадратичною називається функція виду y=ax2+bx+c де a, b, c – задані дійсні числа, при цьому: a≠0.
Розглянуті раніше функції y=x2 і y=ax2 є окремим випадком квадратичної функції:

Графік квадратичної функції y=ax2+bx+c виходить із графіка функції y=ax2, шляхом його паралельного перенесення вгору-вниз і вліво-вправо щодо початку координат – напрямок та величина зміщення графіка залежить від коефіцієнтів b та c.
Головне завдання при побудові графіка квадратичної функції є знаходження координат вершини параболи (x0; y0). Після того, як координати вершини параболи знайдені, вже немає проблем побудувати графік функції y=ax2.
Для швидкого та зручного знаходження координат вершини параболи, що є графіком квадратичної функції виду y=ax2+bx+c, розумні люди застосували метод виділення повного квадрата, завдяки чому квадратична функція була приведена до вигляду:
![]()
Виділення повного квадрата квадратичної функції:

Таким чином, квадратична функція y=ax2+bx+c трансформувалася у функцію виду y=a(x-x0)2+y0, де:
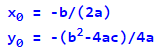
Точка з координатами (x0; y0) є вершиною параболи y=ax2+bx+c
При a>0 гілки параболи спрямовані вгору і квадратична функція в точці (x0; y0) прийматиме мінімум, при a<0 гілки параболи спрямовані вниз і в точці (x0; y0) квадратична функція матиме максимум.
У формулі квадратичної функції коефіцієнт b впливає на зміщення графіка функції, як уздовж осі абсцис, так і уздовж осі ординат; коефіцієнт с – зміщує графік лише вздовж осі ординат.
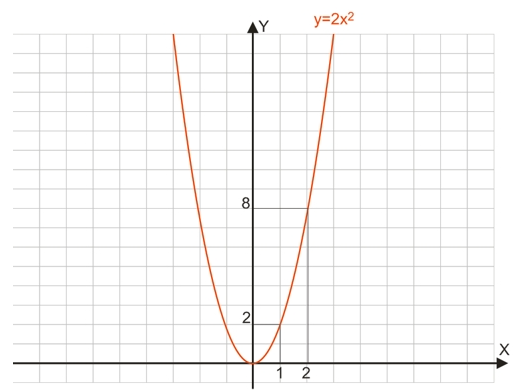
Як приклад збудуємо графік квадратичної функції y=2x2+4x-8.
Графік цієї функції буде отримано шляхом перенесення вершини параболи y=2x2.
Наше завдання – знайти координати вершини функції y=2x2+4x-8.
Це зробити досить просто, використовуючи наведений вище метод виділення повного квадрата квадратичної функції.

Все, що нам залишається зробити – провести паралельне перенесення графіка з початку координат у точку з координатами (-1; -10):
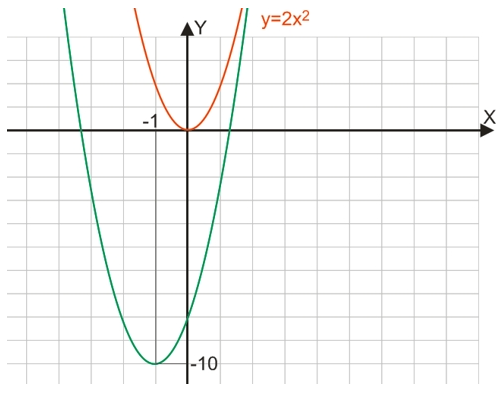
Щоб дізнатися у яких точках графік перетинає вісь абсцис, треба розв’язати квадратне рівняння:


