Формули приведення кутів
Тема “Формули приведення кутів” дуже складна для розуміння. Тому треба кожен випадок розглядати через графічне зображення тригонометричного кола, на якому слід відкладати кути – така наочність значно полегшить засвоєння матеріалу.
Формули приведення дозволяють виразити тригонометричні функції кутів виду:
- π/2+α,
- π+α,
- 3π/2+α,
- 2π+α
через тригонометричні функції кута α.
Навіщо потрібні формули приведення?
Формули приведення дозволяють навести запис тригонометричної функції кута, величина якого лежить у межах 0-90° (0-π/2) – перший квадрант, в якому і синус, і косинус позитивні, що дає можливість з одного боку значно спростити подальші обчислення та спрощення, а з іншого – швидко знайти табличні значення кута.
Наприклад, cos(530°) через формули приведення можна перетворити так:
![]()
На чому ґрунтується принцип формул приведення?
Перше, що треба завжди пам’ятати, – у тригонометрії всі кути мають циклічність в 2π (360 °) – тобто значення всіх тригонометричних функцій кутів, кратних 2π будуть однакові:
- sin(20°)=sin(380°)=sin(740°) і т.д.
- cos(20°)=cos(380°)=cos(740°) і т.д.
- tg (20 °) = tg (380 °) = tg (740 °) і т.д.
- ctg (20 °) = ctg (380 °) = ctg (740 °) і т.д.
Але, крім цього, такі тригонометричні функції кута, як синус і косинус, змінюючись в діапазоні від -1 до +1, залежно від величини кута, мають циклічний характер, тому величини тригонометричних функцій різних кутів, що лежать в діапазоні від 0 до 2π можуть бути рівними.
Наприклад:
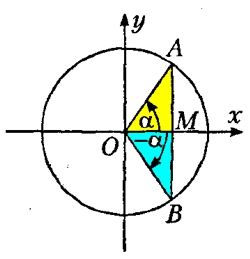
З малюнка дуже добре видно, що абсциси кутів α (AOM) і -α (ВOM) рівні, отже, cos(α)=cos(-α).
Але, кут -α (ВOM), можна уявити, як 2π-α, тому cos(2π-α)=cos(α).
Формули приведення для синусу
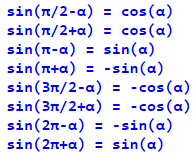
Формули приведення для косинуса
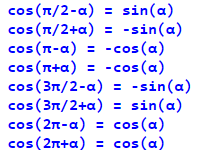
Формули приведення для тангенсу
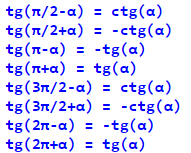
Формули приведення для котангенсу
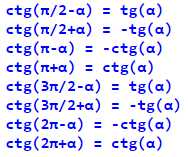
Запам’ятати всі формули наведення досить непросто, бо в них не простежується будь-яка явна закономірність.
Однак, це можна зробити, якщо зрозуміти принцип за яким у приведеній формулі відбувається зміна функції або не змінюється функція на кофункцію і зміна або не зміна знака функції.
Коли треба міняти назву функції у формулі приведення?
Зміна чи не зміна функції у формулі приведення залежить від того, до якого діаметру тригонометричного кола прилягає кут α у формулі приведення.
π/2±α та 3π/2±α це вертикальний діаметр тригонометричного кола (вісь Y), оскільки точки π/2 і π3/2 лежать на осі Y. Якщо помотати головою вгору-вниз, як би ковзаючи поглядом по осі ординат, то автоматично отримаємо відповідь на запитання “чи треба змінювати назву функції у формулі приведення?” – так треба.
π±α та 2π±α це горизонтальний діаметр тригонометричного кола (вісь X), оскільки точки π і 2π лежать на осі Х. Якщо помотати головою вліво-вправо, як би ковзаючи поглядом по осі абсцис, то автоматично отримаємо відповідь на запитання “чи треба змінювати назву функції у формулі приведення ?” – ні не потрібно.
Коли треба міняти знак функції у формулі наведення?
Для відповіді це питання треба знати знаки функцій синуса, косинуса, тангенса і котангенса у кожному квадранті тригонометричного кола.

Для синуса та косинуса – це просто, якщо пам’ятати, що синус – це ордината (Y), а косинус – абсциса (X):
- sin – це вісь Y або вертикальна вісь, тому все, що лежить вище осі абсцис – це “плюс” (I, II квадранти), що лежить нижче – “мінус” (III, IV квадранти);
- cos – це вісь X або горизонтальна вісь, тому, все, що лежить правіше за осі ординат – це “плюс” (I, IV квадранти), що лежить лівіше – “мінус” (II, III квадранти);
- tg і ctg – це відношення синуса і косинуса, тому тангенс і котангенс будуть позитивні в тих квадрантах, в яких синус і косинус мають однаковий знак – це непарні квадранти (I, III); відповідно, у парних квадрантах тангенс та котангенс будуть негативні.
Знак функції у формулі приведення ставиться за квадрантом вихідного кута, при цьому вважаємо, що сам кут є гострим.
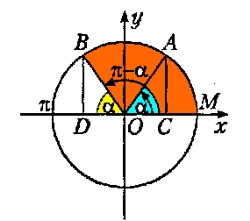
Наприклад, для кута π-α виходить, що кут знаходиться у II квадранті, тому що π-α лежатиме в межах від 90° до 180° (див. рисунок вище). У другому квадранті синус позитивний, тому, у формулі приведення треба буде ставити знак, ідентичний знаку вихідної функції, тобто “плюс”. Оскільки кут π-α прилягає до горизонтального діаметру, то функція не змінюється. Виходить, що sin(π-α) = sin(α).
Для косинуса треба буде змінити знак, тому що у другому квадранті косинус негативний: cos(π-α) = -cos(α).
Для тангенсу та котангенсу: у парному квадранті – знак “мінус”, а функція залишається незмінною:
- tg(π-α) = -tg(α);
- ctg(π-α) = -ctg(α).
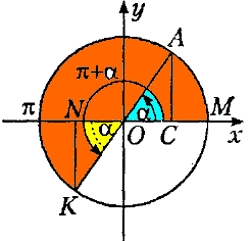
Для кута π+α виходить, що кут знаходиться у III квадранті, тому що π+α лежатиме в межах від 180° до 270° (див. рисунок). У третьому квадранті синус негативний, тому у формулі приведення треба буде змінити знак. Оскільки кут π+α належить до горизонтального діаметра, то функція не змінюється. Виходить, що sin(π+α) = -sin(α). Аналогічно для косинуса: cos(π+α) = -cos(α).
Для тангенсу та котангенсу: у непарному квадранті – знак “плюс”, а функція залишається незмінною:
- tg(π+α) = tg(α);
- ctg(π+α) = stg(α).
Приклад розв’язування рівняння за допомогою формул приведення


