Енергія простого гармонійного руху
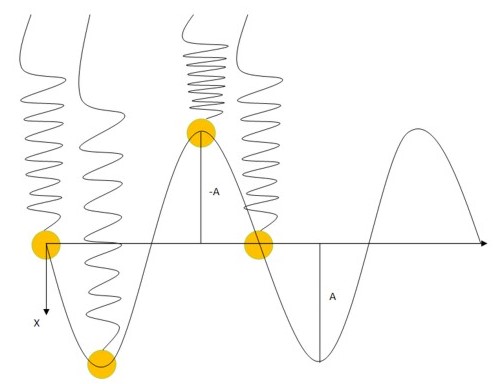
На сторінці “Простий гармонійний рух” розглядався коливальний рух тіла, підвішеного на пружині. У той момент, коли зовнішня сила розтягує пружину з вантажем, вона отримує пружну потенційну енергію, яка потім перетворюється на кінетичну енергію після того, як пружина починає стискатися. Відповідно до закону збереження енергії, який свідчить, що енергія нікуди не дівається безвісти, а переходить з однієї форми в іншу, кінетична енергія тіла перетворюється на пружну потенційну енергію стиснутої або розтягнутої пружини.
У момент, коли пружина з тілом знаходиться у крайній нижній або верхній точці, її потенційна енергія максимальна, а кінетична енергія тіла дорівнює нулю. У момент, коли тіло проходить точку рівноваги, його швидкість максимальна, отже, система тіло+пружина має максимальну кінетичну енергію, при цьому пружина знаходиться в природному стані, і її потенційна енергія дорівнює нулю.
Вирішуємо задачу
З’ясуємо, яка кількість енергії буде запасатися в стиснутій (розтягнутій) пружині.
Під впливом сили F вантаж переміщається на відстань s, виконуючи при цьому роботу А:
![]()
Оскільки в процесі стиснення-розтягування пружини зміна сили F відбувається лінійно з відстанню, її роботу можна представити як добуток середнього значення сили Fср на переміщення s:
![]()
У свою чергу, середня сила є середнім арифметичним сили пружності F1=-kx1 у точці x1 і сили пружності F2=-kx2 у точці x2:
![]()
Переміщення s дорівнюватиме різниці координат точок знаходження вантажу: s=x2-x1.
Підставляючи формулу виразу для s і Fср, отримуємо:
![]()
Оскільки потенційна енергія пружини виражається через формулу: Еy=(kx2)/2, то робота сили пружності пружини дорівнює зміні її пружної потенційної енергії:
![]()
Використовуючи отриману формулу, наприклад, можна дізнатися, наскільки збільшиться пружна потенційна енергія пружини з коефіцієнтом пружності 0,1 Н/м при стисненні її на 0,5 м.
![]()

