Параметри обертального руху
Можливо, що колесо, винайдене людиною давним-давно, стало головним її винаходом, що дозволило вирішити багато інженерних завдань. Розвиток технічного прогресу абсолютно неможливий без колеса та багатьох його похідних.
Основні формули прямолінійного руху та обертального руху
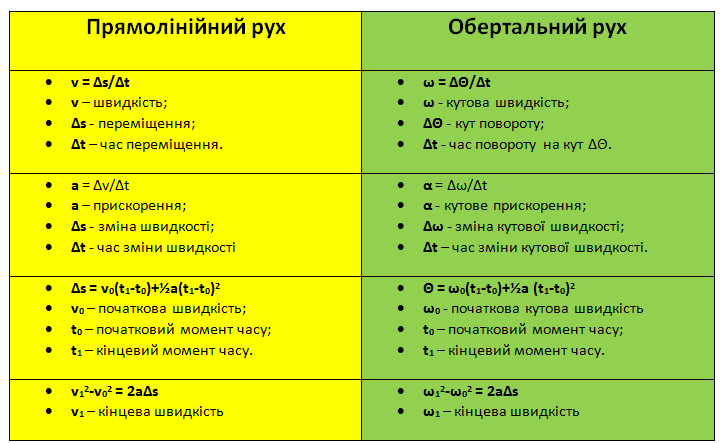
У повсякденному житті більшість об’єктів рухаються складними траєкторіями, які, як правило, складаються з поступального і обертального рухів.
Поступальний рух – це такий рух тіла, при якому будь-яка пряма, пов’язана з об’єктом, що рухається, завжди залишається паралельною самій собі.
Обертальний рух – це такий рух тіла, при якому всі точки тіла рухаються по колу.
У свою чергу, обертальний рух поділяється на тангенційну та радіальну складові:
- Тангенціальний рух – частина обертального руху, якій відбувається за дотичною прямою до кола обертання, швидкість тангенціального руху матеріальної точки називають лінійною швидкістю обертального руху.
- Радіальний (нормальний) рух – частина обертального руху, що відбувається перпендикулярно (за нормаллю) до дотичної прямої або вздовж радіуса кола.
Параметри прямолінійного та обертального рухів можна пов’язати такими формулами:
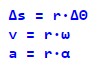
На малюнку нижче представлений приклад обертального руху:
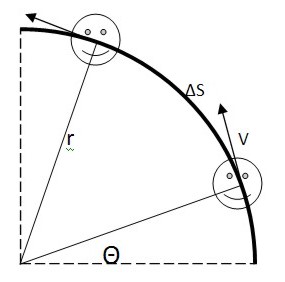
Об’єкт рухається по колу з радіусом r і лінійною швидкістю v, яка є векторною величиною (має величину і напрямок, перпендикулярний радіус-вектору r).
Використовуючи описані вище формули, спробуємо вирішити нескладне завдання і визначити з якою швидкістю рухається автомобіль, якщо його колеса, радіусом 50 см, обертаються з кутовою швидкістю 10 π?
Для вирішення поставленого завдання скористаємося формулою зв’язку лінійної та кутової швидкості:
![]()
Підставимо значення, і отримаємо:
![]()

