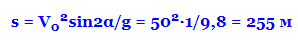Вільне падіння
Вивчаємо вільне падіння на конкретних прикладах. Спробуємо вирішити задачу про Робін Гуда, которий вправно цілив з лука.
Завдання: як високо (далеко) міг стріляти Робін Гуд стрілою вагою 0,1 кг за умови, що його лук дозволяв випускати стрілу з початковою швидкістю 50м/с.
Максимальна висота
Знайдемо максимальну висоту, на яку міг вистрелить Робін Гуд, при умові вертикальної стрільби.
- Початкова швидкість стріли дорівнює: V = 50 м/с.
- Прискорення дорівнює прискоренню вільного падіння: a = g = 9,8 м/с2
У максимально високій точці стріла зупиниться і почне рух вниз: V1 = 0
Знаходимо відстань (висоту) польоту стріли:
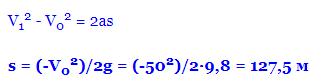
Максимальна висота польоту стріли Робін Гуда становила 127,5 метрів.
Час підйому стріли
А за який час стріла сягне верхньої точки польоту?
Для обчислення скористаємося формулою:

Час підйому стріли на максимальну висоту становить 5,1 секунд.
Можна піти іншим шляхом. У точці максимального підйому швидкість стріли дорівнює нулю. Скористаємося наступним рівнянням:
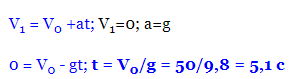
Загальний час польоту стріли займе часу рівно вдвічі більше, оскільки зворотний шлях вниз симетричний прямому шляху вгору.
Максимальна дальність стрілянини
Рух під кутом необхідно розбити на складові по осях X і Y. У нашому випадку сила тяжіння діє тільки вздовж осі Y.
Складові для початкової швидкості:
![]()
Ці складові є незалежними і сила тяжіння діє тільки по осі Y.
- Складова Vx постійна.
- Складова Vy: Vy = V0sinα – gt
Координати стріли у будь-який момент часу по осях:
- Вісь X: x = Vxt = (V0cosα)t
- Вісь Y: y = Vyt – 1/2 · gt2
Загальний час польоту стріли по вертикалі t = 2Vy/g
Можемо дізнатися дальність польоту стріли по осі Х:
![]()
З формули видно, що визначення дальності польоту стріли необхідно знати початкову швидкість стріли і кут пострілу.
Оптимальним для дальності стрільби є кут 45°.
Дійсно: 2sinαcosα = sin2α = max = 1 при sin90°, тобто при α=45°
Дальність стрілянини Робін Гуда: