Гравітація
На поверхні Землі сила тяжіння (гравітація) постійна і дорівнює добутку маси падаючого тіла на прискорення вільного падіння: Fg = mg
Слід зазначити, що прискорення вільного падіння величина стала: g=9,8 м/с2, і спрямована до центру Землі. Тому можна сказати, що тіла з різною масою будуть падати на Землю однаково швидко. Як же так? Якщо кинути з однакової висоти шматочок вати та цеглу, то останній подолає свій шлях до землі швидше. Не забувайте про опір повітря! Для вати воно буде суттєвим, оскільки її густина дуже мала. У безповітряному просторі цегла та вата впадуть одночасно.
Рух похилою площиною
Куля рухається по похилій площині завдовжки 10 метрів, кут нахилу площини 30 °. Якою буде швидкість кулі в кінці площини?
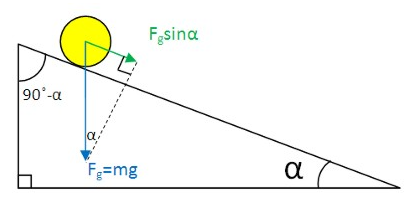
На кулю діє лише сила тяжіння Fg, спрямована вниз перпендикулярно до основи площини. Під дією цієї сили (складової, спрямованої вздовж поверхні площини) куля рухатиметься. Чому дорівнюватиме складова сили тяжіння, що діє вздовж похилої площини?
Для визначення складової необхідно знати кут між вектором сили Fg та похилою площиною.
Визначити кут досить просто:
- сума кутів будь-якого трикутника дорівнює 180 °;
- кут між вектором сили Fg та основою похилої площини дорівнює 90°;
- кут між похилою площиною та її основою дорівнює α
- Виходячи з вищесказаного, шуканий кут дорівнюватиме: 180° – 90° – α = 90° – α
З тригонометрії:
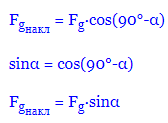
Це дійсно так:
- при α=90° (вертикальна площина) Fgн = Fg
- при α=0° (горизонтальна площина) Fgн = 0
Визначимо прискорення кулі із відомої формули:
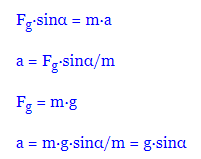
Прискорення кулі вздовж похилої площини не залежить від маси кулі, а лише від кута нахилу площини.
Визначаємо швидкість кулі наприкінці площини:
![]()
(V0=0) – куля починає рух з місця

Зверніть увагу на формулу! Швидкість тіла в кінці похилої площини залежатиме лише від кута нахилу площини та її довжини.
У нашому випадку швидкість 10 м/с наприкінці площини матиме і більярдна куля, і легковий автомобіль, і самоскид, і школяр на санчатах. Звичайно, тертя ми не враховуємо.

