Координати вектора
Будь-який не нульовий вектор a можна виразити через не колінеарні одиничні координатні вектори i, j:
![]()
Оскільки мова зайшла про координатні вектори, не обійтися без прямокутної системи координат.
Напрямок одиничного координатного вектора i (зображений блакитним кольором на малюнку нижче) збігається з позитивним напрямом осі абсцис; вектора j (червоний колір) – з позитивним напрямом осі ординат, причому |i|=|j|=1:
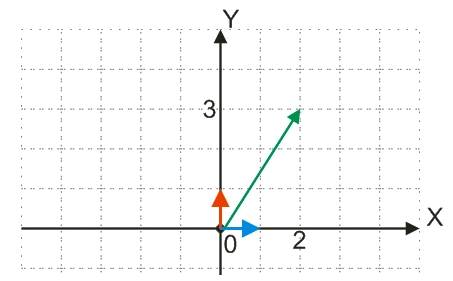
Будь-який вектор a у прямокутній системі координат з координатними векторами i та j, характеризується абсцисою (x) та ординатою (y), де x та y – числа у розкладанні вектора a за векторами i та j.
На малюнку вище вектор (зелений колір) має координати (2; 3) і може бути розкладений через координатні вектори:
![]()
Рівні вектори завжди мають одні й ті самі координати.
При складанні векторів їх координати складаються:
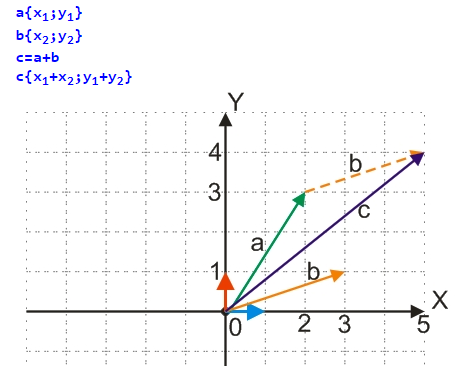
Розглянемо приклад додавання векторів a{2;3} і b{3;1}, зображений на малюнку вище:
![]()
Якщо провести графічні побудови, то з малюнка видно, що координати результуючого вектора с {5; 4}, що збігається з обчисленими за формулою.
При відніманні векторів їх координати віднімаються:

Добуток вектора a{x;y} на число k буде вектором з координатами {kx;ky}.

