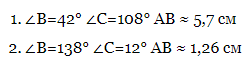Теорема синусів трикутника
Теорема синусів трикутника: Відносини довжин сторін трикутника до протилежних кутів – рівні.
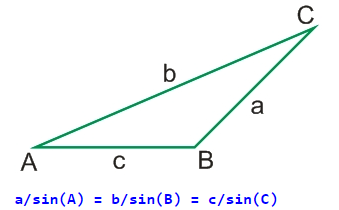
Теорема синусів дозволяє знаходити всі кути та довжини сторін трикутника, якщо відомі:
- два будь-яких кути трикутника і одна з його сторін;
- дві будь-які сторони трикутника і один із двох протилежних їм кутів.
Приклад 1. Побудувати трикутник АВС, у якого відомі одна сторона та два кути: АВ=10 см, ∠B=30°, ∠C=60°.
Рішення. За теоремою синусів:
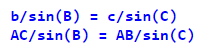
Звідси знаходимо сторону АС:

Для знаходження третьої сторони BC спочатку знайдемо кут А: 180 ° -30 ° -60 ° = 90 °.
Тепер знову використовуємо теорему синусів:

Відповідь: AC = 10/√3; BC = 20/√3; ∠A=90°
Приклад 2. Побудувати трикутник АВС, якщо відомі дві сторони та кут, що протилежить одній з них: ВС = 3 см, AC = 4 см, ∠A = 30°.
Рішення. Відповідно до теореми синусів:

Здавалося б, що завдання вирішене, однак, не треба забувати, що такі тригонометричні функції, як синус і косинус, є дуже “підступними” – нюанс полягає в тому, що значення sin(B)=2/3 ≈ 0,67 можуть набувати два кути в 42 ° і 138 ° (див. Що таке синус).
Фактично з такими даними можуть бути побудовані два трикутники.
З цієї причини, використовуючи теорему синусів, слід знайти обидва варіанти:
Якщо ∠B=42°:

Якщо ∠B=138°:

Відповідь: можна побудувати два трикутники АВС: