Що таке описане коло
Будь-який багатокутник, всі вершини якого належать одному і тому ж колу, називається вписаним у це коло, а саме коло – описаним біля такого багатокутника.
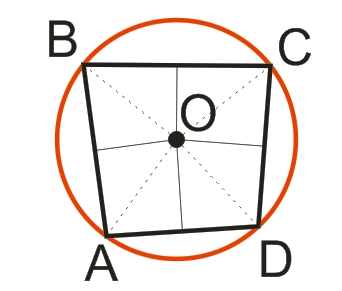
На малюнку зверху зображено чотирикутник ABCD, вписаний у коло (червоний колір) з центром у точці О. Усі вершини чотирикутника лежать на колі. Таке коло називається описаним біля чотирикутника ABCD.
Властивості чотирикутника, вписаного в коло:
- Суми протилежних кутів вписаного чотирикутника дорівнюють: ∠A+∠C=∠D+∠
- Перпендикуляри, проведені через середини сторін вписаного чотирикутника (і взагалі будь-якого описаного багатокутника), перетинаються в точці О, що є центром описаного кола;
- Коло можна описати лише навколо того чотирикутника, суми протилежних кутів якого рівні.
На малюнку нижче зображено трикутник ABC, вписаний у коло (червоний колір) з центром у точці О, – всі вершини такого трикутника лежать на описаному колі.
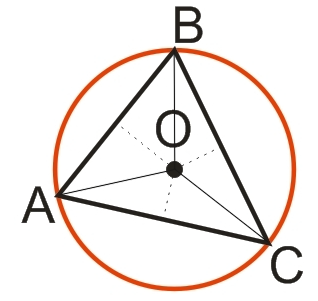
Властивості трикутника, вписаного в коло:
- Навколо будь-якого трикутника можна описати коло і лише одне.
- Перпендикуляри, проведені через середини сторін вписаного трикутника, перетинаються в точці, що є центром описаного кола;
- Відстань від точки перетину серединних перпендикулярів вписаного трикутника до будь-якої з вершин такого трикутника дорівнюватиме радіусу описаного навколо трикутника кола (радіуси OА, OВ, OС).

