Що таке вписане коло
Вписане коло – це коло, яке торкається всіх чотирьох сторін чотирикутника. Таке коло називається вписаним у цей чотирикутник, а сам чотирикутник – описаним біля такого кола.

На малюнку вгорі зображено вписане в чотирикутник ABCD коло (червоний колір), з центром у точці О, яка торкається сторін чотирикутника в точках a, b, c, d.
Властивості чотирикутника, описаного біля кола:
- Суми протилежних сторін описаного чотирикутника дорівнюють: AB+CD=AD+CB.
- Бісектриси всіх кутів описаного чотирикутника (і взагалі будь-якого описаного багатокутника) перетинаються в точці О, що є центром вписаного кола;
- Коло можна вписати лише у той чотирикутник, суми протилежних сторін якого рівні.
- На малюнку нижче зображено вписане в трикутник ABC коло (червоний колір) з центром у точці О, яка торкається сторін трикутника в точках a, b, c.
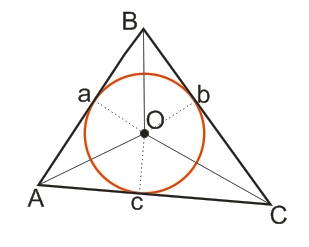
Властивості трикутника, описаного біля кола:
- У будь-який трикутник можна вписати коло і лише одне.
- Бісектриси всіх кутів описаного трикутника перетинаються в точці О, що є центром вписаного кола (бісектриси АО, ВО, СО перетинаються в точці О);
- Відстань від точки перетину бісектрис описаного трикутника до будь-якої зі сторін такого трикутника дорівнюватиме радіусу вписаного в цей трикутник кола (радіуси Oa, Ob, Oc).

