Дотична пряма до кола
Дотична пряма до кола – це пряма, що має лише одну загальну точку з колом (точку дотику).
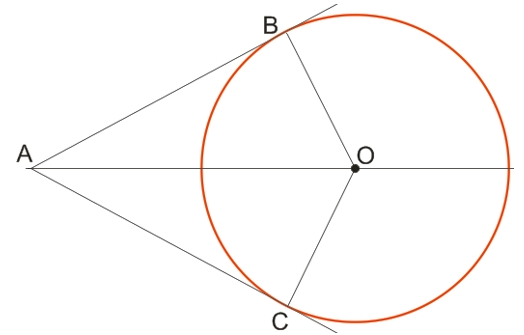
Якщо точка B є точкою дотику прямої AB до кола із центром О, то AB⊥OB.
Якщо AB⊥OB і точка B належить до кола з центром у точці О, то пряма АВ є дотичною до цього кола.
Якщо до кола з центром О провести дві дотичні АВ і АС з однієї точки А, то промінь АО буде бісектрисою кута BAC.
Для доказу треба провести з центру до точок торкання радіуси OB і OC.
Оскільки радіуси OB і OC є перпендикулярами до прямих АВ та АС, то отримаємо два прямокутні трикутники АОВ та АОС із загальною гіпотенузою АО.
Прямокутні трикутники АОВ і АОС будуть рівні, оскільки вони мають загальну гіпотенузу, а катети ОВ і ОС є радіусами одного й того ж кола.
З рівності трикутників випливає рівність сторін АВ і АС, а також рівність кутів BAO і CAO, сума яких становить кут BAC, тому загальна гіпотенуза буде водночас і бісектрисою кута BAC.

