Тангенсоїда {функція виду y=tg(x)}, котангенсоїда y=ctg(x)
Графік функції виду y=tg(x) називається тангенсоїда; графік виду y=ctg(x) – котангенсоїда.
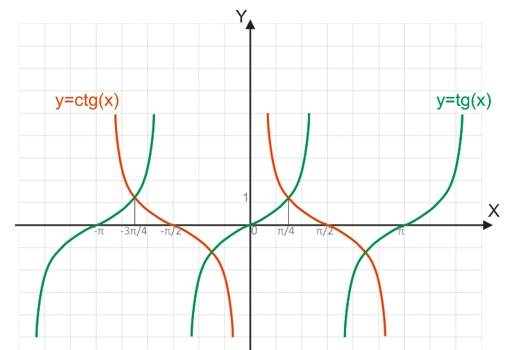
Властивості тангенсоїди та котангенсоїди:
- Область визначення тангенсоїди – область всіх дійсних чисел крім точок, що обертають функцію cos(x) в нуль, тобто, задовольняють умові x=(π/2+kπ) (k – ціле число);
- Область визначення котангенсоїди – область всіх дійсних чисел крім точок, що обертають функцію sin(x) в нуль, тобто, задовольняють умові x=kπ (k – ціле число);
- Функції y=tg(x), y=ctg(x) є періодичними з періодом π. Це дає можливість розглядати будь-який проміжок функцій довжиною в π, при цьому інші проміжки будуть виходити з додавання до нього цілого числа періодів;
- Функція y=tg(x) є зростаючою, зазвичай, дана функція розглядається на проміжку від -π/2 до +π/2;
- Функція y=ctg(x) є спадаючою, як правило, дана функція розглядається на проміжку від 0 до +π;
- Корені функції y=tg(x): усі точки, що задовольняють рівності x=kπ
- Корені функції y=ctg(x): усі точки, що задовольняють рівності x=π/2 + kπ
- Функція y=tg(x) є непарною, тому що tg(-x)=-tg(x) її графік симетричний щодо осі ординат;
- Функція y=ctg(x) є непарною, тому що ctg(-x)=-ctg(x) її графік симетричний щодо осі ординат.
Оскільки, ctg(x)=tg(π2-x)=-tg(x-π/2), то котангенсоїда може бути отримана копіюванням та переносом тангенсоїди на +π/2, при цьому відповідні значення ординати замінюються на протилежні. Простіше кажучи, котангенсоїда є дзеркальним відображенням тангенсоїди щодо вертикальної осі з подальшим зміщенням вправо на π/2.

