Синусоїда {функція y=sin(x)}, косинусоїда y=cos(x)
Графік функції виду y=sin(x) називається синусоїдою; графік виду y=cos(x) – косинусоїдою.
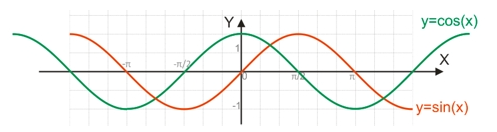
Властивості синусоїди та косинусоїди:
- Область визначення синусоїди та косинусоїди – область всіх дійсних чисел;
- Функції y=sin(x), y=cos(x) є періодичними з періодом 2π. На цьому проміжку максимальне значення, яке можуть набувати обидві функції, дорівнює 1; мінімальне = -1. Це дає можливість розглядати будь-який проміжок функцій довжиною в 2π, при цьому інші проміжки будуть виходити з додавання до нього цілого числа подвоєних періодів;
- Функція y=sin(x) є зростаючою на всіх проміжках, що задовольняють нерівності:
- (-π/2 + 2kπ) ≤ x ≤ (π/2 + 2kπ)
- і спадаючою на всіх проміжках, що задовольняють нерівності:
- (π/2 + 2kπ) ≤ x ≤ (3π/2 + 2kπ)
- (k – ціле число). Див. рисунок вище (червоний графік).
- Функція y=cos(x) є зростаючою на всіх проміжках, що задовольняють нерівності:
- (-π + 2kπ) ≤ x ≤ (2kπ)
- і спадаючою на всіх проміжках, що задовольняють нерівності:
- (2kπ) ≤ x ≤ (π + 2kπ)
- (k – ціле число). Див. рисунок вище (зелений графік).
- Корені функції y=sin(x): усі точки, що задовольняють рівності x=kπ
- Корені функції y=cos(x): усі точки, що задовольняють рівності x=π/2 + kπ
- Функція y=sin(x) є непарною, тому що sin(-x)=-sin(x) її графік симетричний щодо осі ординат;
- Функція y=cos(x) є парною, оскільки cos(-x)=cos(x) її графік симетричний щодо початку координат.
Для побудови синусоїди достатньо збудувати графік функції на відрізку від 0 до π/2. Інші частини повного періоду синусоїди будуть копією побудованого графіка:
- на ділянці від -π/2 до 0 – це буде лінія, симетрична щодо початку координат лінії, побудованої на проміжку від 0 до π/2;
- оскільки sin(π/2-x)=sin(π/2+x), побудований відрізок синусоїди на проміжку від -π/2 до +π/2 буде симетричний щодо осі x=π/2, графіку на проміжку від π/ 2 до 3π/2;
- оскільки cos(x)=sin(π/2+x), то косинусоїда може бути побудована шляхом копіювання та зміщення синусоїди на проміжок (-π/2).

