Ступенева функція (гіпербола), графік ступеневої функції

Властивості функції із натуральним показником y=x^k:

• Область визначення функції y=x^k – область всіх дійсних чисел;
• Якщо k – парне число: функція y=x^k на інтервалі (-∞; 0) є спадаючою та зростаючою на інтервалі (0; ∞);
• Якщо k – непарне число: функція y=x^k на інтервалі (-∞; 0) є зростаючою та спадаючою на інтервалі (0; ∞);
• Корінь функції: x = 0, оскільки графік функції y=x^k проходить через початок координат;
• Функція y=x^k є парною при парному k, тому що (-x)^k=x^k її графік симетричний щодо осі ординат;
• Функція y=x^k є непарною при непарному k, тому що (-x)^k=-x^k її графік симетричний щодо початку координат;
• Функція y=x^k не є періодичною функцією.

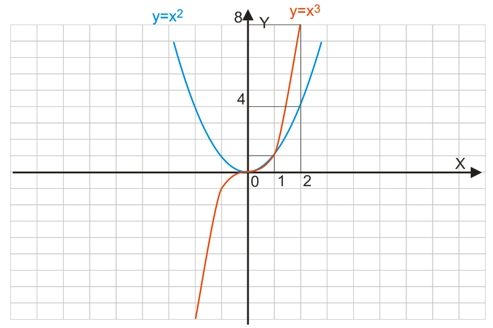
При парному k (графік розташовується в першій та другій координатній чверті – блакитний колір на малюнку) і x≠0 – графік функції y=x^k розташований вище осі абсцис (y>0);

При непарному k (графік розташовується у першій та третій координатній чверті – червоний колір на малюнку):

• при x>0 ордината позитивна (y>0);
• при x<0 ордината негативна (y<0).

Ступенева функція y=x^-1 Гіпербола

Графік функції виду y=x^-1 називається гіперболою.

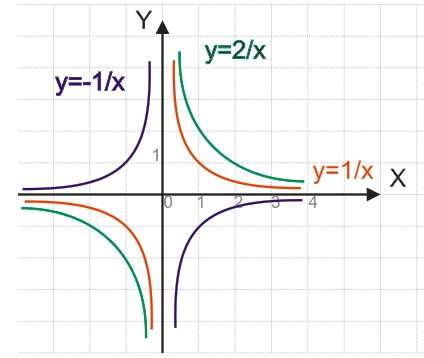
Властивості статечної функції виду y=1/x:

• Область визначення функції y=1/x – область всіх дійсних чисел крім 0;
• Функція  y=1/x є спадаючою на інтервалі від -∞ до 0 (не включаючи) і на інтервалі від 0 (не включаючи) до +∞;
• Функція y=1/x коренів немає, тому, що ділити на нуль не можна, тому графік функції не перетинає вісь абсцис (вісь ординат функція теж не перетинає);
• Функція y=1/x є непарною, тому що 1/(-x)=-(1/x) – її графік симетричний щодо початку координат і розташовується в першій та третій координатних чвертях;
• Функція y=1/x не є періодичною функцією.

Ступенева функція виду y=k/x

Графік ступеневої функції виду y=k/x також має вигляд гіперболи і виходить розтягуванням графіка функції y=1/x від осі абсцис вздовж осі ординат в k раз (див. малюнок вище).

Властивості ступеневої функції виду y=k/x:

• Область визначення функції y=k/x – область всіх дійсних чисел крім 0;
• При k>0 функція y=k/x є спадаючою на інтервалі від -∞ до 0 (не включаючи) і інтервалі від 0 (не включаючи) до +∞;
• При k<0 функція y=k/x зростає на інтервалі від -∞ до 0 (не включаючи) і на інтервалі від 0 (не включаючи) до +∞;
• Функція y=k/x коренів немає, оскільки ділити на нуль не можна, тому графік функції не перетинає вісь абсцис (вісь ординат функція теж не перетинає);
• Функція y=k/x є непарною, тому що k/(-x)=-(k/x) – її графік симетричний щодо початку координат і розташовується в першій і третій координатних чвертях (при k>0) і в другій та четвертій чвертях (при k<0);
• Функція y=k/x не є періодичною функцією.

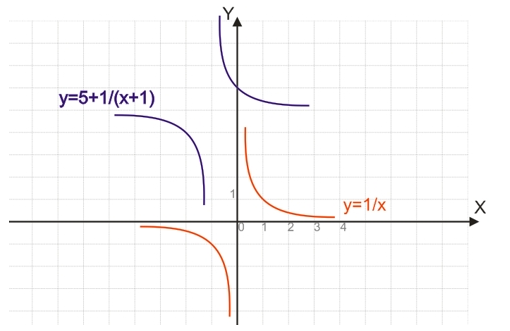
Графік ступеневої функції виду y=a+k/(x+b) виходить з графіка функції y=k/x на а одиниць вгору (при a>0) або вниз (при a<0), а також на b одиниць ліворуч ( при b>0) або праворуч (при b<0).

Індивідуальні заняття з математики в режимі онлайн (Zoom)