Періодичність тригонометричних функцій
Тригонометричні функції – це періодичні функції, оскільки значення цих функцій повторюється через певний період, або, іншими словами, існують певні числа, додавання яких до кута, не змінює значення функції цього кута.
Для синуса та косинуса найменшим періодом є значення 2π (360°), для тангенсу та котангенсу – це значення вдвічі менше: π (180°).
Зрозуміти це дуже просто, якщо знову ж таки звернутися до тригонометричного кола. Накресливши повне коло, ми знову потрапимо у вихідну точку, тобто значення синуса і косинуса кутів 0° і 360° будуть однакові, оскільки, на колі це буде та сама точка.
Щоб знайти значення функції, аргумент якої перевищує 360° (2π), треба відняти цілу кількість періодів, що вкладаються в аргумент:
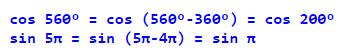
Вирішимо більш складне завдання, знайшовши найменший період для функції y=sin(x+1/2π).
Нехай k – найменший період цієї функції, додавання якого до аргументу х, значення функції не змінить:
![]()
Розглянемо аргумент (x+1/2π), як єдине ціле. У такому разі найменшим періодом буде значення 2π:
![]()
Тепер можна знайти найменший період для нашого завдання:


