Переміщення, швидкість та прискорення – векторні величини
Переміщення, швидкість та прискорення – це векторні величини. Тепер, маючи нові знання про вектори, можна перевести скалярні рівняння у векторну форму:
![]()
Повний вектор переміщення – це комбінація переміщення з початковою швидкістю та переміщення з постійним прискоренням.
Ми розглянули два способи опису векторів для вирішення фізичних завдань.
- Перший спосіб заснований на використанні складових по осях Х і Y.
- Другий спосіб – на величині (модулі) та напрямку вектора.
Формула перетворення двох способів опису векторів:
![]()
де α – кут між горизонтальною складовою та гіпотенузою L
Якщо відомі складові (x; y), то величину вектора та його напрямок можна визначити за формулами:
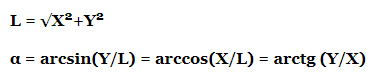
Завдання
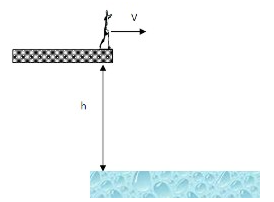
Олексій Середа виконує стрибок у воду з 10-метрової вежі (h=10м), маючи під час відштовхування горизонтальну швидкість V=2 м/с. Визначте швидкість Олексія під час входження у воду і як далеко це буде від краю вежі?
Рішення задачі
З умови завдання випливає, що компоненти швидкості спортсмена рівні (2; 0) і він знаходиться за 10 метрів від поверхні води. У процесі падіння він рухатиметься із постійним прискоренням g=9,8м/с2 (прискорення вільного падіння).
Визначаємо відстань “приводнення” від краю вежі.
Оскільки прискорення відбувається тільки у вертикальній площині (вісь Y), то компонент швидкості Vx не змінюється. Отже, відстань по горизонталі = Vx t, де t – час польоту спортсмена.
Переміщення по вертикалі з урахуванням тяжіння Землі:
![]()
Знаходимо час польоту спортсмена:
![]()
Тепер можемо визначити відстань приводнення від краю вежі:
![]()
Спортсмен увійде у воду на відстані 2,8 метра від краю вежі.
Тепер перейдемо до визначення швидкості спортсмена під час входження у воду.
Ми знаємо, що компонента швидкості Vx незмінна (2;0).
По осі Y сила тяжіння Землі прискорила спортсмена – нам треба визначити величину компоненти швидкості стрибуна по вертикалі:
![]()
Vy0 – початкова вертикальна швидкість = 0
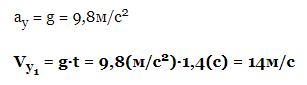
Але оскільки g є вектором, спрямованим до центру Землі (тобто, вниз – від’ємний напрямок осі Y), то на поверхні землі вектор g=-9,8м/с2:
![]()
Компоненти кінцевої швидкості спортсмена = (2; -14) м/с. Розмір вектора швидкості (з теореми Піфагора):
![]()
Відповідь:
- Швидкість спортсмена при вході у воду приблизно дорівнює 14,1 м/с
- Відстань входження у воду від краю вежі – 2,8 м.

