Що таке синус, косинус, тангенс, котангенс

Розглянемо коло, центр якого збігається з центром координат, а радіус дорівнює ОА:

 

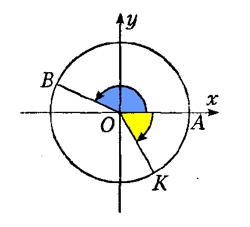
Повернувши радіус ОА проти годинникової стрілки, отримаємо кут АОВ. Такий кут називається позитивним (на малюнку виділено синім кольором).

Повернувши радіус ОА за годинниковою стрілкою, отримаємо кут АОК. Такий кут називається негативним (на малюнку виділено жовтим кольором).

Тепер візьмемо позитивний кут АОВ, отриманий поворотом радіуса ОА проти годинникової стрілки на деякий кут α (зафарбований жовтим кольором):

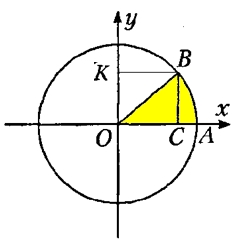
Синусом кута AOB (або α) називають відношення ординати точки (відрізок ОК=ВС) до довжини радіуса ОВ:

Косинусом кута AOB (або α) називають відношення абсциси точки (відрізок ОС) до довжини радіуса ОВ:

Тангенсом кута АОВ називають відношення синуса цього кута до його косинусу:

Котангенсом кута АОВ називають відношення косинуса цього кута до його синуса:

Оскільки, у формулах тангенсу та котангенсу присутній поділ, то тангенс та котангенс не завжди можна визначити, оскільки на нуль ділити не можна.

• Тангенс кута неможливо визначити, коли косинус цього кута набуває нульового значення, – це всі кути 90°+180°·n або π/2+π·n, де n-будь-яке ціле число.
• Котангенс кута неможливо визначити, коли синус цього кута набуває нульового значення, – це всі кути 0°+180°·n або π·n, де n-будь-яке ціле число.

Неважко помітити, що кут α, що розглядається нами, є центральним гострим кутом прямого трикутника СОВ – його вершина збігається з початком координат, а величина менше 90°. При цьому один з катетів (ОС) трикутника СОВ розташований на осі абсцис.

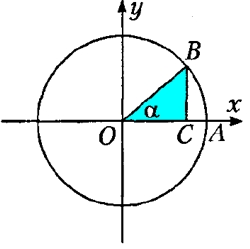
У такому випадку, протилежний куту α катет ВС є ординатою вершини В, що лежить на колі, а прилеглий катет ОС – абсцисою вершини В, при цьому гіпотенуза ОВ буде радіусом кола.

Враховуючи цю обставину, визначення синуса, косинуса, тангенсу та котангенсу кута α прямокутного трикутника СОВ формулюватимуться наступним чином:

• Синусом кута α (sin α) називають відношення протилежного до кута α катета до гіпотенузи: ВС/ОВ;
• Косинусом кута α (cos α) називають відношення катета, що прилягає до кута α, до гіпотенузи: ОС/ОВ;
• Тангенсом кута α (tg α) називають відношення протилежного до кута α катета до прилеглого: ВС/ОС;
• Котангенсом кута α (ctg α) називають відношення катета, що прилягає до кута α, до протилежного: ОС/ВС;

Зверніть увагу на важливу обставину – тригонометричні величини sin, cos, tg, ctg не залежать від величини радіуса кола (довжини гіпотенузи прямокутного трикутника), а залежать лише від величини кута α. Тому, в тригонометрії вважають, що розглянутий кут є центральним кутом кола з радіусом, рівним умовній одиниці (так зване коло з одиничним радіусом): r=1.

У такому випадку, для вершини, розташованої на колі з одиничним радіусом, можна сказати, що:

Слід запам’ятати значення синуса, косинуса, тангенсу та котангенсу для “стандартних” кутів, які зустрічатимуться найчастіше:

• α = 0°
  • sin α = 0
  • cos α = 1
  • tg α = 0
  • ctg α – не існує
• α = 30 ° (π / 6)
  • sin α = 1/2
  • cos α = √3/2
  • tg α = √3/3
  • ctg α = √3
• α = 45°(π/4)
  • sin α = √2/2
  • cos α = √2/2
  • tg α = 1
  • ctg α = 1
• α = 60°(π/3)
  • sin α = √3/2
  • cos α = 1/2
  • tg α = √3
  • ctg α = √3/3
• α = 90°(π/2)
  • sin α = 1
  • cos α = 0
  • tg α – не існує
  • ctg α = 0