Вектори
Ніхто не буде сперечатися, що до місця призначення неможливо дістатися не знаючи напряму руху. У фізиці це поняття називається вектором. До цього моменту ми з вами оперували деякими числами та значеннями, які називаються величинами. Вектор відрізняється від величини наявністю напряму.
Працюючи з вектором оперують його напрямом і величиною. Фізичний параметр без урахування напряму називають скаляром.
Візуально вектор відображається у вигляді стрілки. Довжина стрілки – величина вектора.
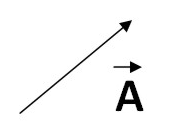
У фізиці для позначення векторів використовують велику букву зі стрілкою нагорі.
Вектори можна порівняти. Два вектори будуть рівні, якщо вони мають однакову величину та напрямок.
Додавання векторів
Вектори можна складати. Результуючий вектор є сумою обох векторів і визначає відстань та напрямок. Наприклад, ви мешкаєте у Дніпрі і вирішили відвідати старих друзів у Києві, а звідти зробити візит до улюбленої тещі до Чернівців. Наскільки далеко ви перебуватимете від рідного дому, гостюючи у мами дружини?
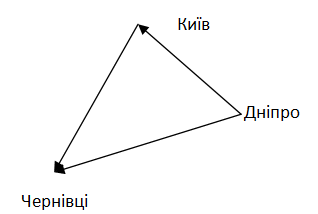
Для відповіді на це запитання вам треба накреслити вектор від вихідної точки подорожі (Дніпро) та до кінцевої (Чернівці). Новий вектор визначає результат усієї подорожі від початку і до кінця.
- Вектор А – Дніпро – Київ
- Вектор В – Київ – Чернівці
- Вектор С – Дніпро – Чернівці
С = А+В де С – сума векторів або результуючий вектор
Віднімання векторів
Вектора можна не лише складати, а й віднімати! Для цього треба поєднати основи від’ємника і від’ємного векторів і з’єднати їх кінці зі стрілками:

- Вектор А = С-В (Дніпро-Київ) = (Дніпро-Чернівці) – (Київ-Чернівці)
- Вектор В = С-А (Київ-Чернівці) = (Дніпро-Чернівці) – (Дніпро-Київ)
Вектори та числа
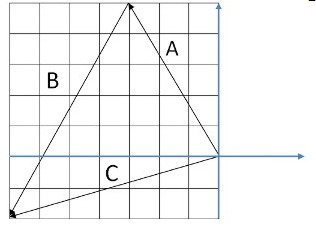
Накладемо на наші вектори координатну сітку. Для вектора А можна сказати, що він спрямований на 5 клітин вгору (позитивне значення осі Y) і на 3 клітини вліво (від’ємне значення осі Х): X=-3; Y=5.
Для вектора В: напрямок на 4 клітини вліво і 7 клітин вниз: X=-4; Y=-7.
Т.ч., для складання векторів по осях X та Y треба скласти їх координати. Щоб отримати координати результуючого вектора по осях X та Y:
А(-3;5) + В(-4;-7) = С(-7;-2)
Координати вектора
Розглянемо завдання: куля рухається зі швидкістю 10м/с по похилій площині з довжиною основи X=1м, розташованої під 30° до горизонту. Потрібно визначити час, за який куля переміститься від початку до кінця площини.
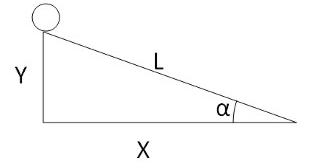
У цій задачі швидкість є вектором V з величиною 10м/с і напрямом = 30° до горизонталі. Щоб визначити швидкість переміщення кулі вздовж основи похилої площини, нам треба визначити X -складову переміщення кулі, яка є скаляром (має тільки значення, але не напрямок) і позначається Vx. Аналогічно, Y – складова швидкість також скаляр і позначається Vy. Вектор швидкості через складові: V = (Vx; Vy)

Визначимо складові (Vx; Vy). Згадуємо тригонометрію:
![]()
Х – складова швидкості кулі:
![]()
Горизонтальна швидкість кулі дорівнює 8,66 м/с.
Довжина основи похилої площини дорівнює 1м, то цю відстань куля подолає за:
![]()
Т.ч., кулі знадобиться 0,12с для переміщення вздовж похилої площини.
Відповідь: 0,12с
Визначимо Y – складову швидкості:
![]()
Оскільки час “подорожі” кулі однаковий для обох складових, то можемо визначити висоту Y, з якої котилася куля:
![]()
Відстань, пройдена кулею:
![]()
Зворотне завдання
Розглянемо завдання, обернене попередньому:
Куля перемістилася вздовж похилої площини на висоту 0,6м, при цьому у горизонтальній площині переміщення склало 1,0м. Необхідно знайти відстань, пройдену кулею та кут.
Відстань обчислюємо за теоремою Піфагора:
![]()
По тригонометрії:
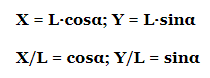
Тепер можна знайти кут:
![]()
Підставляємо цифри:
![]()
Проміжне обчислення L можна виключити: