Система двох рівнянь із двома невідомими

Системою двох рівнянь із двома невідомими називають два спільно розглянуті рівняння, з одними й тими самими невідомими

Рішенням системи рівнянь із двома невідомими буде пара чисел, при підстановці яких у кожне із рівнянь системи вони перетворюються на істинні рівності.

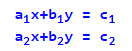
Наприклад, рішенням наступної системи рівнянь будуть числа x = 2; y=3:

Кажуть, що пара чисел (2; 3) є рішенням системи рівнянь, що розглядається.

Слід розуміти, що такі рівняння, як, наприклад, x=2; y=3 можна розглянути, як систему двох рівнянь із двома невідомими. Дійсно:

Інша справа, що таку систему і вирішувати не треба, бо одразу відомі змінні x і y. Але такі уявлення треба знати і пам’ятати, оскільки, в деяких випадках вони допомагають знайти розв’язання складніших систем рівнянь.

Вирішувати систему двох рівнянь із двома невідомими можна кількома способами.

Спосіб підстановки

Ідея способу підстановки полягає в тому, що в одному з рівнянь одне невідоме виражається через інше, після чого підставляється на друге рівняння, в якому виходить тільки одне невідоме.

Зрозуміти цей вислів не так вже й просто, тому, краще все продемонструвати на простенькому прикладі.

У другому рівнянні виражаємо одне невідоме через інше:

Тепер у нас вийшла нова система рівнянь, в якій одне з рівнянь перейшло з початкової системи рівнянь, а друге отримано підстановкою цього рівняння невідомого, виражене через інше невідоме:

Таким чином ми позбулися у другому рівнянні від невідомого x:

Друге рівняння тепер представлене у вигляді 0x+b·y = c:

Знаходимо рішення другого рівняння:

Тепер залишилося підставити числове значення змінної y до першого рівняння і знайти x:

Нову систему рівнянь, що вийшла, можна представити у вигляді двох рівнянь з двома невідомими:

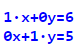
Оскільки всі проведені нами перетворення рівностей були тотожними, початкова система рівнянь буде рівносильна фінальної, а, отже, мати те саме коріння (5; 6), яке і буде рішенням початкової системи рівнянь.

При вирішенні системи двох рівнянь з двома невідомими способом підстановки не має значення, яке невідоме виражати через інше – результат буде один і той же.

Спосіб складання

Ідея рішення залишається незмінною – позбутися одного з рівнянь одного з невідомих. Шлях досягнення цієї мети у способі додавання полягає в підборі коефіцієнтів, на які треба помножити обидві частини рівнянь, щоб коефіцієнти при одному з невідомих були однакові за модулем, але різні за знаком. Після цього рівняння складаються і вирішується нова система рівнянь, яка буде тотожною початковій, оскільки всі операції, що проводяться, тотожні.

Як і в першому випадку, позбудемося у другому рівнянні від невідомої y, для цього помножимо обидві частини другого рівняння на 6:

Тепер складаємо перше та друге рівняння, і отримуємо нову систему рівнянь:

У новій системі рівнянь перше рівняння взято із початкової системи, а друге є сумою рівнянь після виконаних перетворень. Подальший хід рішення повністю аналогічний способу підстановки:

Графічний спосіб розв’язання

Кожне з рівнянь, що входять до системи, можна розглядати як формулу, яка задає певну функцію.

Оскільки функція має свій графік, який задається її формулою, його можна побудувати на координатній площині.

Так як рівняння у нас лінійні, то і графік лінійної функції буде у вигляді прямої.

В результаті ми отримаємо дві прямі координати точки перетину яких і будуть рішенням нашої системи рівнянь.

Треба сказати, що до цього методу вдаються досить рідко, оскільки він досить незручний і  дає приблизні результати.