Арифметичний квадратний корінь
У математиці кожна дія має свого “антипода”, у складання є віднімання, у множення – розподіл. “Антиподом” зведення в ступінь є витяг кореня з числа.
Так, якщо до 3 додати 2, то вийде 5, а якщо з 5 відняти ті ж 2, то отримаємо 3. Те саме вийде, якщо 3 помножити на 2, а потім результат множення (6) розділити на 2. Якщо 3 звести в другий ступінь – отримаємо 9, щоб отримати назад із дев’яти трійку, необхідно витягти з 9 квадратний корінь.
Арифметичним квадратним коренем числа А називається таке число m, що: m2=A, при цьому m≥0
Вилучення кореня з числа позначається позначкою √:
![]()
Оскільки вирази √A=m та А=m2 є тотожними, то вираз √A = m має сенс лише за m≥0, тому, що неможливо отримати негативне число множачи його на само себе.
Квадратний корінь добутку та дробу
Квадратний корінь добутку невід’ємних множників дорівнюватиме добутку коренів із цих множників:

Квадратний корінь із дробу, у якого чисельник невід’ємний, а знаменник позитивний, дорівнюватиме дробу чисельник якого дорівнює кореню квадратному із чисельника, а знаменник – кореню квадратному із знаменника:
![]()
Винесення та внесення множника з під знака кореня
Правило винесення множника з під знака кореня:

Правило внесення множника під знак кореня:
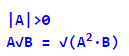
Квадратний корінь зі ступеня
За будь-якого значення А буде вірна наступна рівність:

За будь-яких позитивних А і В (A≠B):
- якщо A<B, то √A<√B
- якщо A>B, то √A>√B
![]()

